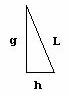
h = horizontal component of acceleration = g tan b
[L = lift vector]
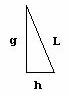
h = horizontal component of acceleration = g tan b
[L = lift vector]
The position vector for a circle is r = (R cos q)i + (R sin q)j where R is the radius of the circle and q is the angle with the positive x-axis. If va is the angular velocity in radians per second, then q = vat where t is time, so
r = (R cos vat)i + (R sin vat)j Differentiating, we get:
v = dr/dt = (-Rva sin vat)i + (Rva cos vat)j and
a = dv/dt = (-Rva2cos vat)i + (-Rva2 sin vat)j = -Rva2[(cos vat)i + (sin vat)j]
Now the length of this vector is Rva2 = R·va· va
If vais in radians per second, the aircraft velocity v is va·R, so va = v/R
Substituting for one of the va factors, we have the length of the acceleration vector is
|a| = va·v
This must be equal to g tan b from the figure above. Thus we have
g tan b = va·v
so tan
b = ![]()
Now va is in radians per second, g and
v are in feet per second. We must apply some conversion factors here. Let
D be the turn rate in degrees per second and let s be the aircraft’s speed
in knots. Then![]() and
and![]() (1
NM = 6076 ft) giving
(1
NM = 6076 ft) giving
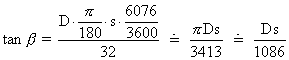
It must be remembered when using a computer that the
arctan function gives results in radians, so the result must be multiplied
by ![]() after
the arctan is computed to get the bank angle in degrees. A 3o
per second turn requires a bank angle of 15.4o at 100 knots.
after
the arctan is computed to get the bank angle in degrees. A 3o
per second turn requires a bank angle of 15.4o at 100 knots.