THE GOLDEN RATIO IS IRRATIONAL
An Algebraic Proof
First, let's start with an assumption (actually two assumptions).
The golden ratio is between 1 and 2.
Neither of these assumptions is difficult to prove.
Now let's assume there are positive integers x and y such that the golden ratio is equal to
 . Then 1 <
. Then 1 <  < 2 so y < x < 2y which gives 0 < x-y < y. We may either assume at this point that
< 2 so y < x < 2y which gives 0 < x-y < y. We may either assume at this point that
 is in reduced form, or we may skip that assumption (the
finishing touches of the proof are different, but the middle section is identical in either case).
If we do make the assumption that
is in reduced form, or we may skip that assumption (the
finishing touches of the proof are different, but the middle section is identical in either case).
If we do make the assumption that  is reduced, it
is worth noting that the reduced form of a rational number is the form with the smallest positive denominator.
is reduced, it
is worth noting that the reduced form of a rational number is the form with the smallest positive denominator.
The definition of the golden ratio implies that 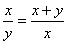
Now a little algebra:
x2=xy + y2
x2-xy = y2
x(x-y)=y2
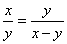
Thus if  is equal to the golden ratio, then
there is another representation of the same number that has a smaller positive denominator.
If we assumed earlier that
is equal to the golden ratio, then
there is another representation of the same number that has a smaller positive denominator.
If we assumed earlier that  is reduced, then
we have a contradiction. Otherwise, note that we could apply the same logic to
is reduced, then
we have a contradiction. Otherwise, note that we could apply the same logic to
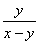 to find a fraction also equal to the golden ratio
with a still smaller positive denominator. Since there are only a finite number of positive integers less than y,
this process cannot continue indefinitely which gives us a contradiction.
to find a fraction also equal to the golden ratio
with a still smaller positive denominator. Since there are only a finite number of positive integers less than y,
this process cannot continue indefinitely which gives us a contradiction.
 Return to Bob's Homepage
Return to Bob's Homepage
 Aurora University Homepage
Aurora University Homepage
Date last modified: 7/1/04
Send me mail
 . Then 1 <
. Then 1 <  < 2 so y < x < 2y which gives 0 < x-y < y. We may either assume at this point that
< 2 so y < x < 2y which gives 0 < x-y < y. We may either assume at this point that
 is in reduced form, or we may skip that assumption (the
finishing touches of the proof are different, but the middle section is identical in either case).
If we do make the assumption that
is in reduced form, or we may skip that assumption (the
finishing touches of the proof are different, but the middle section is identical in either case).
If we do make the assumption that  is reduced, it
is worth noting that the reduced form of a rational number is the form with the smallest positive denominator.
is reduced, it
is worth noting that the reduced form of a rational number is the form with the smallest positive denominator.
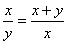
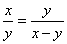
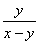 to find a fraction also equal to the golden ratio
with a still smaller positive denominator. Since there are only a finite number of positive integers less than y,
this process cannot continue indefinitely which gives us a contradiction.
to find a fraction also equal to the golden ratio
with a still smaller positive denominator. Since there are only a finite number of positive integers less than y,
this process cannot continue indefinitely which gives us a contradiction.