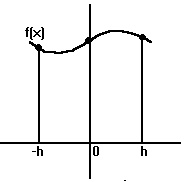
To make this discussion easier, we can translate the y-axis so that it passes through the point x_j+1 without changing the shape of the curves involved, the width of the intervals, or the results of any of the computations. Since Simpson's rule uses equally spaced intervals, we can now label the point that was originally x_j+1 as 0 and then label x_j as -h and x_j+2 as +h as shown. Now the cubic polynomial f(x) has the general form ax³+bx²+cx+d, and the quadratic polynomial generated by Simpson's rule has the general form ex²+fx+g. The error function then is E(x)=ax³+bx²+cx+d-(ex²+fx+g) which has the general form px³+qx²+rx+s, and the integral of E(x) from -h to h is the error in the Simpson method within this interval. Now since the quadratic polynomial agrees with f(x) at the endpoints and midpoints, we have E(-h)=E(0)=E(h)=0. Evaluating E(0) we have s=0, so E(x) actually has the form px³+qx²+rx   Evaluating E(-h) and E(h), we get:
E(-h)=-ph³+qh²-rh=0
E(h)=ph³+qh²+rh=0     and adding these two equations together gives
2qh²=0
Since h is not zero, we must have q=0, so E(x) has the form E(h)=px³+rx
But this means E(x) is an odd function [that is, E(-x)=-E(x), so E(x) is symmetric about the origin], and therefore

In summary, this shows that when Simpson's rule is used to generate a quadratic approximation to a cubic polynomial over two subintervals, the quadratic polynomial underestimates the area under the cubic in one subinterval and overestimates it by the same amount in the other subinterval. This is one of those rare cases when two wrongs really do make a right!

It may still be a gift from the god of mathematics, but perhaps this gives a more intuitive feel for the phenomenon.

Return to Bob's Homepage
Aurora University Homepage

Date last modified: 5/8/00