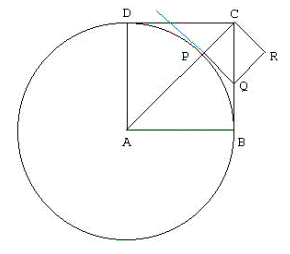
Construct a square ABCD as shown. Draw the diagonal AC. Now if AC and AB are commensurable, then there is a line segment of some length, say r, such that AC=m₁r and AB=m₂r where m₁ and m₂ are integers. Now draw a circle centered at A with radius AB. Note that CB and CD are tangent to this circle [why?]. This circle intersects AC at some point; call it P. Now obviously AP=AB, so PC=AC-AB= m₁r - m₂r= (m₁ - m₂)r so PC is also an integer multiple of r and is therefore commensurable with AB and AC. Construct the tangent to the circle at P. Note that this tangent is perpendicular to AC. This tangent intersects BC at some point; call it Q. Now Angle(PCQ)=45^o=Angle(PQC) so Triangle(PQC) is an isosceles triangle and therefore PC=PQ. We can construct a square with vertices C, P, and Q; call the fourth vertex R (see the figure above). 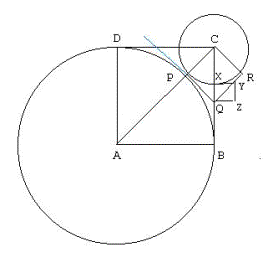Now since QP and QB are tangents to a circle from an external point, they are equal, so QB=QP=PC=(m₁ - m₂)r=m₄r where we have set m₄= m₁ - m₂. Then QC=BC-QB=m₂r - m₄r=(m₂ - m₄)r=m₃r (with m₃=m₂ - m₄) so QC is also commensurable with AB and AC. We now have a new square whose side and diagonal are commensurable with AB and AC. We note that m₁>m₂>m₃>m₄. There's no reason we can't do the same thing on square PCRQ. We can draw a circle centered at C with radius CP, call the intersection of this circle with CQ point X, construct the tangent there, and construct square XYZQ as shown. Then the side and diagonal of this square are commensurable with AB and AC as well. Then we can continue the process indefinitely constructing smaller and smaller squares with sides and diagonals commensurable with AB and AC. However, there are only a finite number of integer multiples of r less than m₁r, so we have a contradiction.

Had we looked a little more carefully at QB in the above figure, we would have discovered that its length is equal to (2m₂-m₁).  This leads to a "Two-For-One" proof that the square root of 2 is irrational.  The difference between the two proofs is a slight change in assumptions at the beginning which leads to a different ending, but the algebra in the middle is identical.

Proof 1	Common Statements	Proof 2
	Assume that the square root of 2 is rational.  Then there exist positive integers a and b such that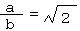
		Assume that a/b is in reduced form.  This is equivalent to saying that a/b is the representation of this rational number with the smallest positive denominator.
	Now a little algebra:      a2=2b2 a2-ab=2b2-ab a(a-b)=b(2b-a)
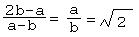We now have a fraction equal to a/b with a smaller positive denominator than b.		We now have a fraction equal to a/b with a smaller positive denominator than b which is a contradiction.
Let a'=2b-a and b'=a-b.  We can use the same procedure to find a'' and b'' so that a/b=a'/b'=a''/b'' with b>b'>b''>0.  There's no algebraic reason we can't continue this process indefinitely.  However, there are only a finite number of positive integers less than b, so we have a contradiction.

In the book The Golden Ratio by Mario Livio, the author suggests that due to their interest in the pentagram and pentagon, the Pythagoreans may have discovered the incommensurability of the side and diagonal of the pentagon before they discovered the incommensurability of the side and diagonal of a square. If this theory is true, then the irrationality of the golden mean (PHI) was discovered before the irrationality of the square root of 2. See Chapter 2 and Appendix 2 of the book for details, and see this page for a similar, but somewhat simpler proof.

Return to Bob's Homepage
Aurora University Homepage

Date last modified: 12/23/02