A Geometric Proof that the Golden Ratio is Irrational
In his book The Golden Ratio Mario Livio proposes that the first number
discovered to be irrational is the golden ratio. His proof is something that
might have been discovered accidentally by the Pythagoreans while they were investigating
properties of their beloved pentagram and the associated pentagon.
A somewhat simpler proof that the golden ratio is irrational than that of
Livio's involves an acute golden triangle (a triangle in which the ratio
of the sides to the base is the golden ratio).
First, we need to understand that the Pythagoreans did not think of rational numbers
as the ratio of two integers as we do.
They thought of two line segments as "commensurable" if both were an integer multiple
of some smaller length. Thus a line segment of length 3/8 and a line segment of
length 5/6 were commensurable since they were both integer multiples of a line segment
of length 1/24. They assumed all pairs of line segments were commensurable (which is
the same as assuming all numbers are rational). Their discovery that the golden ratio
is irrational may have gone something like this
(note that all required constructions can be done with a straightedge and compass as
preferred by Greek mathematicians):
First, note that if two line segments are commensurable, then the sum
and the difference of the two segments are also commensurable (since
the sum and difference of two positive integers is also an integer).
Begin with an isosceles triangle in which the peak angle is 36o
and the base angles are 72o.
Construct the angle bisector of one
of the base angles as shown. Since half of 72 is 36, DBC=36o
and
BDC=72o. Thus triangle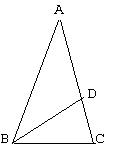 BDC is similar to triangle ABC. Since
angle ABD = angle BAD, triangle ABD is isosceles, so AD=BD=BC,
and therefore DC is the difference of commensurable segments. Thus if
AB
and BC are
commensurable, then DC is commensurable using the same unit of
commensurability. Therefore the sides and diagonal of triangle BDC are
commensurable using the same unit of commensurability as that used in
triangle ABC. We can continue this process by bisecting one of the base
angles of triangle BDC to get a smaller similar triangle in which the
sides and base are also commensurable using the same unit of
commensurability, then a still smaller triangle, and so on.
Eventually, the side of one of these triangles will be shorter than the
original unit of commensurability which leads to a contradiction.
To see that the ratio of the
sides to the base of triangle ABC (and therefore also triangle BDC) is the
golden ratio, note that AC/BC=BC/DC by similarity, but then
AC/AD=AD/DC which is the geometric definition of the golden ratio.
BDC is similar to triangle ABC. Since
angle ABD = angle BAD, triangle ABD is isosceles, so AD=BD=BC,
and therefore DC is the difference of commensurable segments. Thus if
AB
and BC are
commensurable, then DC is commensurable using the same unit of
commensurability. Therefore the sides and diagonal of triangle BDC are
commensurable using the same unit of commensurability as that used in
triangle ABC. We can continue this process by bisecting one of the base
angles of triangle BDC to get a smaller similar triangle in which the
sides and base are also commensurable using the same unit of
commensurability, then a still smaller triangle, and so on.
Eventually, the side of one of these triangles will be shorter than the
original unit of commensurability which leads to a contradiction.
To see that the ratio of the
sides to the base of triangle ABC (and therefore also triangle BDC) is the
golden ratio, note that AC/BC=BC/DC by similarity, but then
AC/AD=AD/DC which is the geometric definition of the golden ratio.
Triangle ADB is an obtuse golden triangle in which the ratio of the base
to the sides is the golden ratio. It has a peak angle of
108o
and base angles of 36o. To prove that this is a golden triangle,
find a point E on AB so that BDE=36o. Then BED=108o,
and you can work out the similarities, equalities, and ratios from there.
The same kind of proof as above is possible with golden rectangles. If you remove a square
from a golden rectangle, the remaining smaller rectangle is also a golden rectangle whose
side and base are commensurable with the side and base of the original rectangle using the
same unit of commensurability. There's another one you can work out for yourself!
It is also possible to construct an algebraic
proof that the golden ratio is irrational that has some
similarities to the geometric proof.
 Return to Bob's Homepage
Return to Bob's Homepage
 Aurora University Homepage
Aurora University Homepage
Date last modified: 8/18/03
Send me mail
 BDC is similar to triangle ABC. Since
angle ABD = angle BAD, triangle ABD is isosceles, so AD=BD=BC,
and therefore DC is the difference of commensurable segments. Thus if
AB
and BC are
commensurable, then DC is commensurable using the same unit of
commensurability. Therefore the sides and diagonal of triangle BDC are
commensurable using the same unit of commensurability as that used in
triangle ABC. We can continue this process by bisecting one of the base
angles of triangle BDC to get a smaller similar triangle in which the
sides and base are also commensurable using the same unit of
commensurability, then a still smaller triangle, and so on.
Eventually, the side of one of these triangles will be shorter than the
original unit of commensurability which leads to a contradiction.
To see that the ratio of the
sides to the base of triangle ABC (and therefore also triangle BDC) is the
golden ratio, note that AC/BC=BC/DC by similarity, but then
AC/AD=AD/DC which is the geometric definition of the golden ratio.
BDC is similar to triangle ABC. Since
angle ABD = angle BAD, triangle ABD is isosceles, so AD=BD=BC,
and therefore DC is the difference of commensurable segments. Thus if
AB
and BC are
commensurable, then DC is commensurable using the same unit of
commensurability. Therefore the sides and diagonal of triangle BDC are
commensurable using the same unit of commensurability as that used in
triangle ABC. We can continue this process by bisecting one of the base
angles of triangle BDC to get a smaller similar triangle in which the
sides and base are also commensurable using the same unit of
commensurability, then a still smaller triangle, and so on.
Eventually, the side of one of these triangles will be shorter than the
original unit of commensurability which leads to a contradiction.
To see that the ratio of the
sides to the base of triangle ABC (and therefore also triangle BDC) is the
golden ratio, note that AC/BC=BC/DC by similarity, but then
AC/AD=AD/DC which is the geometric definition of the golden ratio.